SVM原理简介：最大间隔分类器

SVM是一种二类分类模型，其求解目标在于确定一个分类的超平面，以最大化特征空间上的间隔。分类超平面的确定只取决于少数的样本信息，这些关键的样本被称之为支持向量Support Vector，这也是SVM–支持向量机名称的由来。

首先我们举一个二维空间的小例子，并假设样本是线性可分的，这样我们就可以在二维空间里划一条直线（高维空间的超平面在二维空间表现为直线），完全分开所有的正负样本。那么引出一个问题，显然存在多条区分正负样本的直线（例如下图的实线和虚线），哪条是更好的选择？

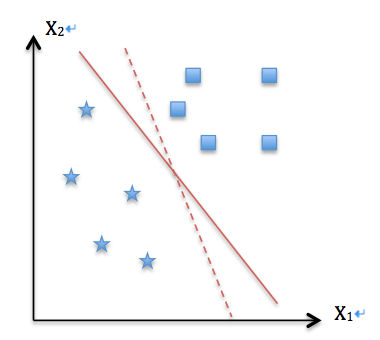
从直观上我们希望正负样本分得越开越好，也就是正负样本之间的几何间隔越大越好。这是因为距离分类超平面越近的样本，分类的置信度越低（实际上几何间隔代表了分类器的误差上界）。SVM的优化目标，正是最大化最接近分类超平面的点到分类超平面的距离。
我们把这个二维的分类超平面设为$f(x)=w^Tx+b=0$。把样本$x$代入$f(x)$中，如果得到的结果小于0，我们对该样本标一个-1的类别标签$y_i$，大于0则标一个+1的$y_i$。（约定为+1或-1只是为了下面的推导便利而已）。
首先定义函数间隔（function margin）：

$\widehat{\gamma}=|w^Tx+b|=y_i(w^Tx+b)$

注意前面乘上$y_i$可以保证这个margin的非负性（因为$f(x)<0$对应$y_i=-1$的那些样本）。
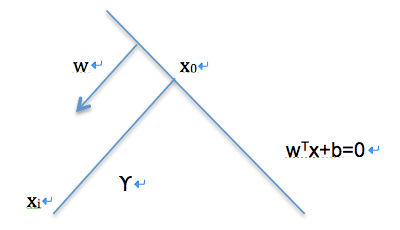
如下图所示，对任意不在分类超平面上的点$x_i$，我们可以依赖它到分类超平面的垂直投影$x_0$，计算出它到分类超平面上的几何间隔（geometrical margin）：

$\widetilde{\gamma}=\frac{|w^Tx_i+b|}{||w||}=\frac{y_i(w^Tx+b)}{||w||}=\frac{\widehat{\gamma}}{||w||}$

（$||w||$是向量$w$的范数，是对$w$长度的一种度量）。于是我们得到了函数间隔和几何间隔的数值关系。

假定所有样本到分类超平面的函数间隔最小值表示为$\widehat{\gamma}$，我们可以把SVM的优化问题描述成以下表达式：
$\max \widetilde{\gamma}=\widehat{\gamma}/||w||, s.t. y_i(w^Tx+b)>=\widehat{\gamma}, i=1, …, n$
由于$\widehat{\gamma}$和$||w||$是线性关联的，而即便在超平面固定的情况下，$||w||$仍是可变化的（只要$b$随着$||w||$等比缩放，比如$x_1+x_2+1=0$和$2x_1+2x_2+2=0$其实是一个平面），那么$\widehat{\gamma}$实际上不影响SVM优化问题的求解，为了简化问题，我们设$\widehat{\gamma}=1$，从而把优化问题转化为：

$\max \widetilde{\gamma}=1/||w||, s.t. y_i(w^Tx+b)>= 1, i=1, …, n$

这个问题可以转化为一个等价的二次规划问题，也就是说它必然能得到一个全局的最优解。
通过求解这个问题，我们可以得到了一个最大化几何间隔的分类超平面（如下图红线所示），另外两条线到红线的距离都等于$1/||w||$，而橘黄色的样本就是支持向量Support Vector。

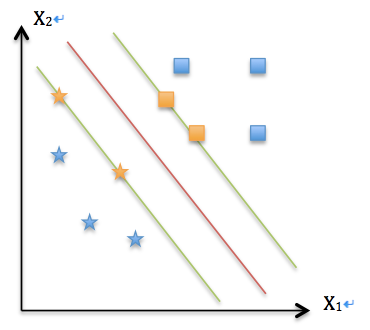
到此为止，通过最大化几何间隔，使得该分类器对样本分类时有了最大的置信度，准确的说，是对置信度最小的样本有了最大的置信度，这正是SVM的核心思想。