卡方检验原理及应用

卡方检验，或称x2检验，被誉为二十世纪科学技术所有分支中的20大发明之一，它的发明者卡尔·皮尔逊是一位历史上罕见的百科全书式的学者，研究领域涵盖了生物、历史、宗教、哲学、法律。之前做文本分类项目用过卡方值做特征选择（降维），后来听内部培训，另一个部门说他们有用卡方检验做异常用户的检测，于是就想把卡方检验再温习一次，同时把卡方检验和特征选择串起来理解。

无关性假设

举个例子，假设我们有一堆新闻标题，需要判断标题中包含某个词（比如吴亦凡）是否与该条新闻的类别归属（比如娱乐）是否有关，我们只需要简单统计就可以获得这样的一个四格表：

组别	属于娱乐	不属于娱乐	合计
不包含吴亦凡	19	24	43
包含吴亦凡	34	10	44
合计	53	34	87

通过这个四格表我们得到的第一个信息是：标题是否包含吴亦凡确实对新闻是否属于娱乐有统计上的差别，包含吴亦凡的新闻属于娱乐的比例更高，但我们还无法排除这个差别是否由于抽样误差导致。那么首先假设标题是否包含吴亦凡与新闻是否属于娱乐是独立无关的，随机抽取一条新闻标题，属于娱乐类别的概率是：(19 + 34) / (19 + 34 + 24 +10) = 60.9%

理论值四格表

第二步，根据无关性假设生成新的理论值四格表：

组别	属于娱乐	不属于娱乐	合计
不包含吴亦凡	43 * 0.609 = 26.2	43 * 0.391 = 16.8	43
包含吴亦凡	44 * 0.609 = 26.8	44 * 0.391 = 17.2	44

显然，如果两个变量是独立无关的，那么四格表中的理论值与实际值的差异会非常小。

x2值的计算

x2的计算公式为：

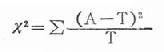
其中A为实际值，也就是第一个四格表里的4个数据，T为理论值，也就是理论值四格表里的4个数据。

x2用于衡量实际值与理论值的差异程度（也就是卡方检验的核心思想），包含了以下两个信息：

• 实际值与理论值偏差的绝对大小（由于平方的存在，差异是被放大的）
• 差异程度与理论值的相对大小

对上述场景可计算x2值为10.01。

卡方分布的临界值

既然已经得到了x2值，我们又怎么知道x2值是否合理？也就是说，怎么知道无关性假设是否可靠？答案是，通过查询卡方分布的临界值表。

这里需要用到一个自由度的概念，自由度等于V = (行数 - 1) * (列数 - 1)，对四格表，自由度V = 1。

对V = 1，卡方分布的临界概率是：

显然10.01 > 7.88，也就是标题是否包含吴亦凡与新闻是否属于娱乐无关的可能性小于0.5%，反过来，就是两者相关的概率大于99.5%。

应用场景

卡方检验的一个典型应用场景是衡量特定条件下的分布是否与理论分布一致，比如：特定用户某项指标的分布与大盘的分布是否差异很大，这时通过临界概率可以合理又科学的筛选异常用户。

另外，x2值描述了自变量与因变量之间的相关程度：x2值越大，相关程度也越大，所以很自然的可以利用x2值来做降维，保留相关程度大的变量。再回到刚才新闻分类的场景，如果我们希望获取和娱乐类别相关性最强的100个词，以后就按照标题是否包含这100个词来确定新闻是否归属于娱乐类，怎么做？很简单，对娱乐类新闻标题所包含的每个词按上述步骤计算x2值，然后按x2值排序，取x2值最大的100个词。